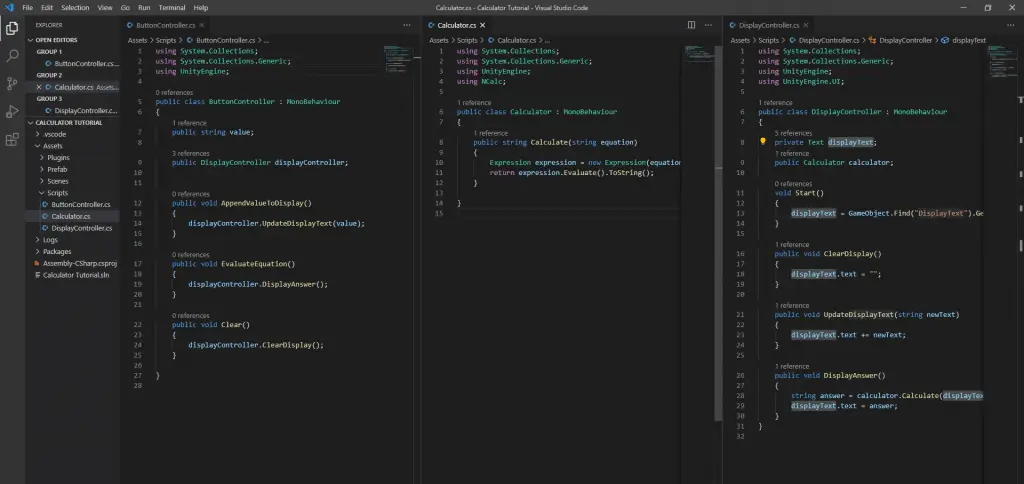
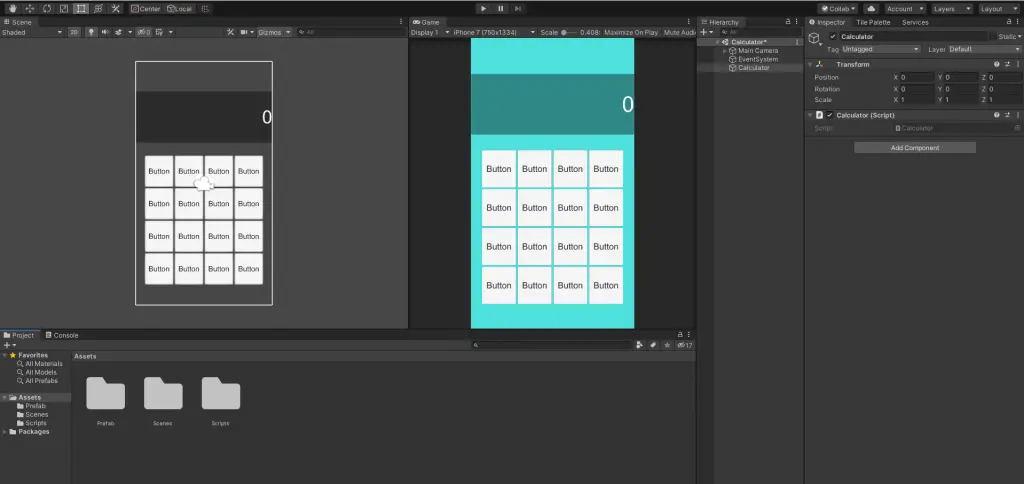
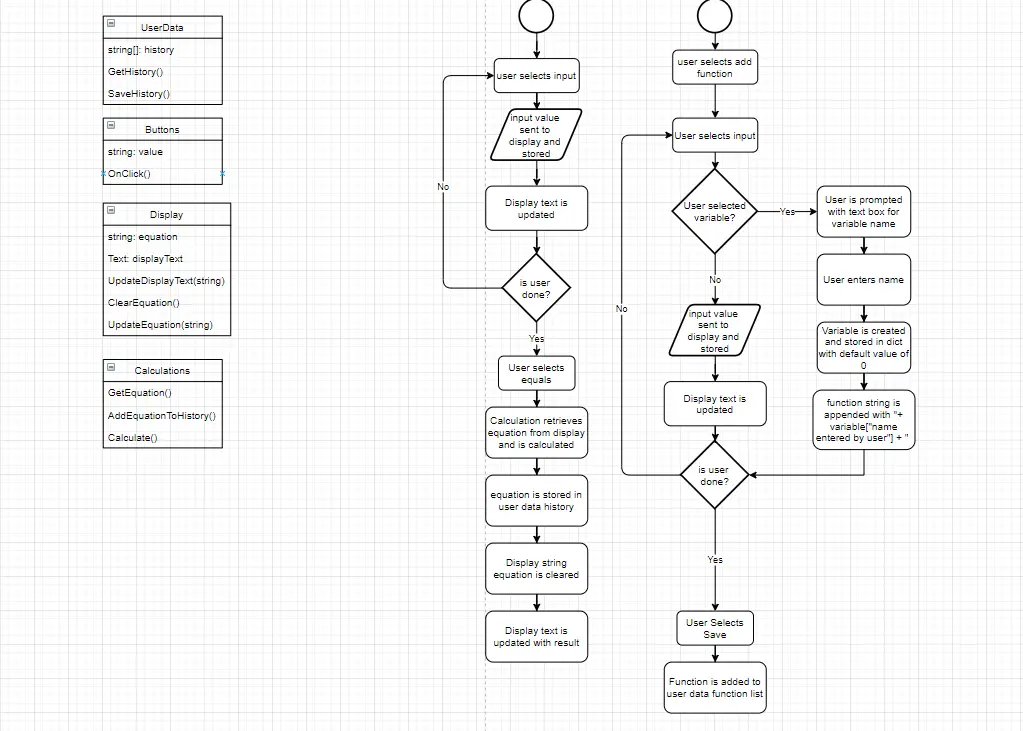
Best Free and Open Source Game Engines
Best Free and Open Source Game Engines Introduction Developing a game can be a daunting task because there are so many things to consider like what language to program it in, what tools should you use, cost, compatibility, and so on. One of the main tools you will need when developing a game is a …